There are no sounds that you can define purely in terms of their harmonic spectra. Even if a sound seems to exhibit a consistent tone and volume, there must have been a moment when it began, and a moment when it will end. This implies that the loudness of the sound is contoured in some fashion.
Let’s try to make this idea a bit more meaningful. Imagine that the amplifier in Figure 1 is your hi-fi amp, and that — although the tone generator is generating a signal — the volume knob is turned fully anticlockwise so that you hear no sound. Imagine you now turn the control fully clockwise while the sound is playing, and then turn it back anticlockwise again until silence returns.
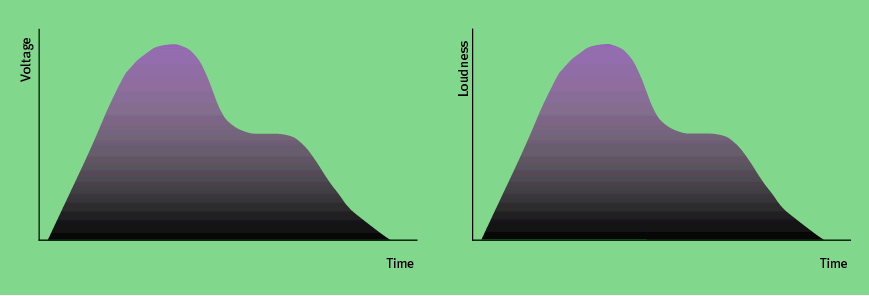
Let’s say that, if the knob is turned fully anticlockwise, the applied CV is 0 Volts, and the amplifier’s Gain is zero. In other words, silence reigns. At the other extreme, let’s say that, if the knob is rotated fully clockwise, the CV is 10V, and the Gain is maximum — ie. the sound is at its loudest. You could then imagine using the knob to apply varying voltages to create a loudness ‘contour’ for our sound. For example, the CV could start at 0 Volts, rise to 10V, drop to 5V, linger there for a while, before returning to 0V some time later. This profile is shown in Figure.
As you can see, the contour of the CV is identical to the loudness contour. In other words, you have defined the loudness of the sound at any given time using the CV. The shapes in Figure are called Envelopes.